Recently I was watching The Imitation Game and thoguht it would be fun to write an implementation of the Enigma Machine (based on Enigma I) as well as a blog post about it.
The Basics
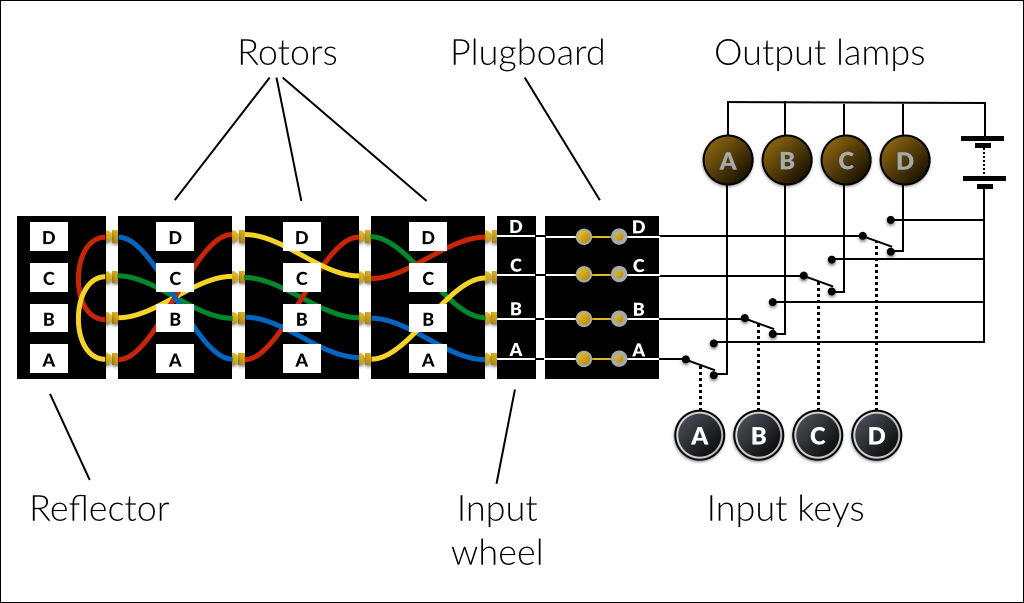
The Enigma machine was a complex electro-mechanical encryption device used by the German military during World War II to encode their communications. It was invented by Arthur Scherbius in 1918 and was based on the principles of rotor cipher machines. It was designed to be extremely secure, and it used a variety of techniques to prevent unauthorized access to its messages (More on this later)
It had a keyboard that consisted of 26 letters, a space bar, and a few punctuation marks. The output of the machine was displayed on a lamp board, which also had 26 letters. The operator would type the message on the keyboard, and the scrambled output would appear on the lamp board.

The Rotors
The basic principle behind the Enigma machine was to use a series of rotating wheels (rotors) to scramble the letters of a message. Each rotor had 26 contacts, one for each letter of the alphabet, and a series of electrical contacts on the inside. The rotors were mounted on a spindle and could be rotated in any order.
When a letter was typed on the keyboard, it was sent through a series of electrical connections that passed through the rotors. The first rotor would change the letter to another letter based on its position, and then the output of the first rotor would be passed through the second rotor, which would again change the letter to another letter based on its position. This process would continue until the message was scrambled by all of the rotors.
But how many possible paths does that give us through three rotors for the letter A? Keep in mind that each rotor can be turned to any position. That means that for the first rotor there are 26 possible paths through it for A. But once we’ve followed the wire through the first rotor, there are now 26 possible paths through the second rotor. And then 26 more possible paths through the third one. The total possible number of paths for A to take through all three rotors is therefore 26*26*26 = 17,576. Considering each rotor is wired differently and assuming we have 5 rotors to chose from for a 3 roter machine we have a choice out of 5 to use for the first one, then a choice out of the 4 for the second one, and then a choice out of 3 for the last one. That gives 60 possible ways to choose the three rotors. This gives us a total of 17576*60 = 1054560 possibilities.
The output of the rotors was then sent through a reflector, a fixed rotor that does not move during the encryption process, and whos purpose is to ensure that the same input letter is never encoded as itself (this ended up making the machine vulnerable to certain cryptographic attacks, which were ultimately exploited by the Allies ). The reflector works by reflecting the signal back through the rotors in a way that scrambles the signal further.
Rotor Offsets
To increase the complexity of the encryption, the Enigma machine uses rotor offsets, which are the initial positions of the rotors before encryption begins. The rotors in the Enigma machine have notches that allow the rotor to advance one position after each keystroke. By changing the initial position of the rotors, the encryption can be made more complex, and the same letter can be encrypted differently depending on the rotor settings.
Ring Settings
In the Enigma machine, the ring setting is an additional setting that further increases the complexity of the encryption. The ring setting is related to the notches on the rotor and determines which contact points on the rotor will be engaged with the electrical contacts on the other rotors during encryption. Each rotor in the Enigma machine has a series of notches cut into its circumference. These notches control when the rotor advances by one position during encryption, causing a shift in the electrical contacts engaged with the other rotors. By changing the position of the ring, the notches on the rotor are shifted relative to the starting position, which changes the electrical connections and further complicates the encryption. The ring setting is a letter, and it represents the position of the rotor relative to the electrical contacts on the Enigma machine. For example, if the ring setting is "A," then the rotor is in its default position, and its notches are aligned with the electrical contacts on the Enigma machine. If the ring setting is "B," then the notches on the rotor will be shifted by one position relative to the starting position, and the electrical connections will be different. The ring setting is usually set along with the rotor offset before encryption begins, making it challenging for anyone without knowledge of the correct settings to decrypt the message. The German military changed the ring setting and rotor offset settings daily during World War II, further complicating the encryption and making it extremely challenging for the Allies to decode intercepted messages.
The Plugboard
To further enhance the security of the Enigma machine, it had a plugboard. The plugboard allowed the operator to swap letters before they were encrypted, adding another layer of complexity to the encryption process. The plugboard had ten pairs of plugs that could be used to swap letters, effectively increasing the number of possible configurations of the machine. Since there are 26 letters, up to 13 swaps can be done but typically only 10 were used. The plugboard was the main reason for the machine's very high number of possible outputs. The number of possible ways to connect the plugboard is now 150,738,274,937,250. Multiplying that by the other possible combinations above, we get that the overall number of possible paths a letter can take is 158,962,555,217,826,360,000.

To decode an Enigma message, the receiver needed to know the exact settings of the rotors and the plugboard. The Germans changed these settings every day, which meant that the Allies had to break the code every day. The codebreakers at Bletchley Park in England, led by Alan Turing, were able to break the Enigma code by using a combination of mathematics, statistics, and a lot of hard work. You can find an implementation of the Enigma Machine, specifically Enigma I, on my github.
